(506) 2240-6804
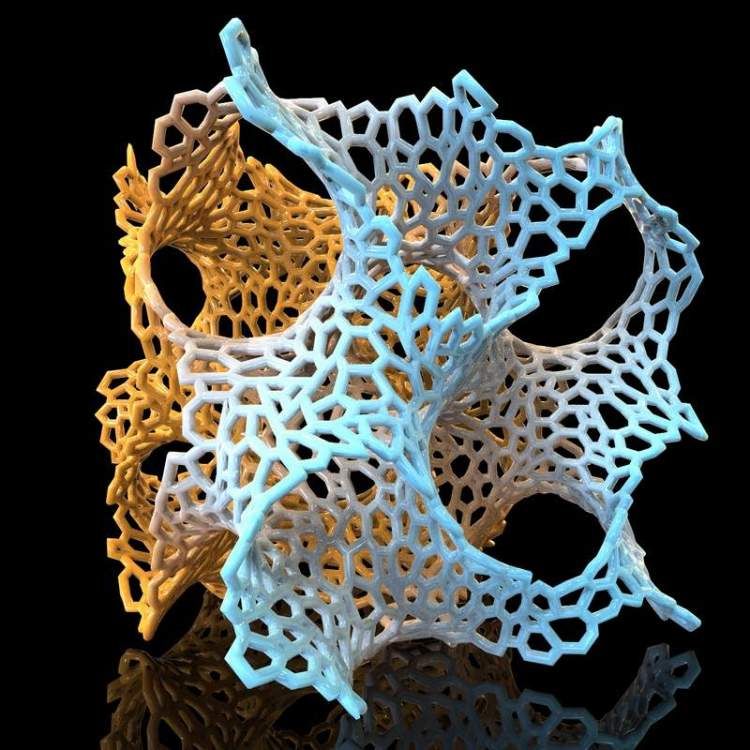
Sierpinski pyramid 3d print
▷ fractal pyramid 3d models 【 STLFinder 】
Fractal Pyramid
thingiverse
Fractal Pyramid
Fractal Pyramid
cults3d
pyramid
Fractal pyramid
thingiverse
This was inspired by [ octahedron fractal IFS thing v1 and 2](https://www.thingiverse.com/thing:2818824). This was made with Structure Synth. ...Remove '//' in the 'Main' section for some variations.
Super Duper Fractal Pyramid
prusaprinters
. .. and beyond!</p> <p>Tell us the predicted print time on your printer, if your slicer doesn't crash! Better yet, print one for super duper bragging rights! Print instructionsUnassociated tags: fractal pyramid, super duper Category: Math Art
Super Duper Fractal Pyramid
thingiverse
We upgraded the excellent Sierpinski Fractal Pyramid to a higher level! Fractals are shapes that repeat themselves over and over again as you magnify them, just like a broccoli. To infinitesimal and beyond! Tell us the predicted print time on...
Symmetric Fractal Pyramid
thingiverse
None of the fractal pyramids on Thingiverse were symmetrical.
This one is. That's the whole story. Enjoy!
I don't actually have a Creality, I have an Artillery SWX1, but that's not an option. needless to say, its scaled for a 300x300mm bed.
Fractal Pyramid Wall Hanging
thingiverse
Fractal Pyramid modified for wall hanging. Flattened and transformed into a diamond shape. This is sized for a 300mm bed. I don't know if it will work scaled down. Even though it uses spiral vase mode, it is a long print (24+ hours). First layer...
Fractal Pyramid - Multi Color
thingiverse
Remix of the fractal pyramid split into multiple sections.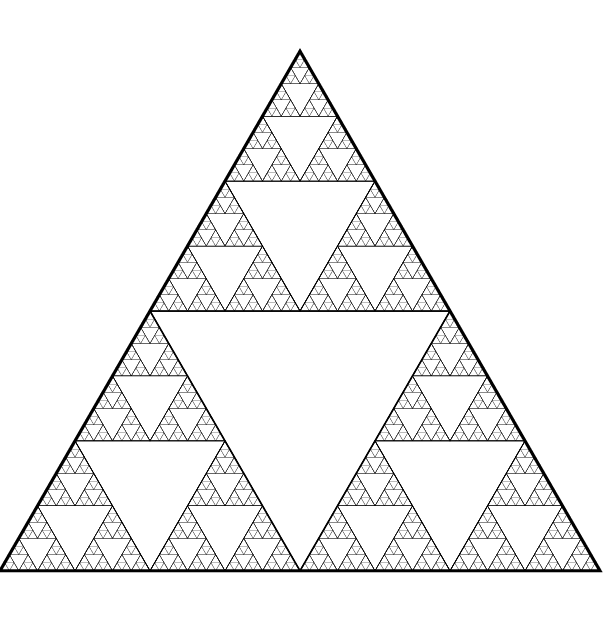
*Note* - Use the .3mf files to import into cura or your slicer of choice (or windows 3d builder) they should load pre-stacked that way. Otherwise you may have to arrange the stl's...
Super Duper Fractal Pyramid (Revised)
cults3d
We upgraded the excellent Sierpinski Fractal Pyramid to a higher level! Fractals are shapes that repeat themselves over and over again as you magnify them, just like a broccoli. To infinitesimal and beyond! Tell us the predicted print time on your...
Fractal Pyramid Lamp and Base
thingiverse
I really loved the look of the fractal pyramid and wanted to turn it into a lamp so i designed a base for it that will house a led strip and print the pyramid with transparent filament to turn it into a lamp.
I imagine a glow in the dark filament...
Stand for Sierpinski Octahedron / Flake Fractal Pyramid
thingiverse
The octahedron is made from ricktu's Fractal Pyramid, print it twice and stick together. https://www.thingiverse.com/thing:1356547/files NOTE THIS STAND IS FOR the file "Pyramid 6" the largest one DrLex stand gave some inspiration. The...
Fractal pyramid / tetrahedron
prusaprinters
<p>There are a variety of these available already but I wanted something that could easily be modified. This will print with “addinvert=false;” but only if bridging works very well.
...I managed to print this without supports on a Prusa Mini.</p>
Large Fractal Pyramid
thingiverse
x 4.5 BIGGER
Fractal pyramids (Egypt)
thingiverse
Fractal pyramids (Egypt). Designed in Wolfram Methematica. ...Post-printing processing is not required.
Fractal Pyramid with Continuous Cross-section
thingiverse
Every triangular face is a Sierpinski triangle, and the base of the pyramid is (approximately) a space-filling curve called the Sierpiński curve.
Figures like the Vicsek fractal also exist in this model. Print Settings Printer Brand: ...
Mandelbulb 3D Fractal - Simple Pyramid
prusaprinters
Hi there, here is another 3D Fractal. Fractals seem to me like Rohrschach tests, everybody can see something different in them, like in the ink blobs. Design The Fractal is made with - Mandelbulb 3D get this fascinating piece of opensource software...
Fractal Ball Pyramid with Captive Spheres
thingiverse
This is a 3D fractal loosely based on the 3D Sierpinski gasket. The octahedral voids that the 3D Sierpinski gasket are recursively filled with arrangements of spheres.
If the recursion were to go infinite, it would create the sharp edges of the...
Mandelbulb - Arrow Pyramid Fractal
thingiverse
______________________________________________________________________ Design The Fractal is made with - Mandelbulb 3D get this fascinating piece of opensource software at: https://www.mandelbulb.com/ Julius Horsthuis, Hal Tenny and Don Whitaker...
Mandelbulb - Arrow Pyramid Fractal
prusaprinters
To me it looks like arrows forming a Pyramid. Design The Fractal is made with - Mandelbulb 3D get this fascinating piece of opensource software at: https://www.
mandelbulb.com/ Julius Horsthuis, Hal Tenny and Don Whitaker have many good Tutorials...
Pyramid Spiral Fractal
thingiverse
This fractal was created for a JMU 3D Printing class. ... It is a pyramid shrinking and spiraling into itself https://geekhaus.com/math203_fall2017/2017/09/19/tinkercad-fractal-3/
Serpinski Pyramid Fractal with 1 iteration on each face.
thingiverse
Each face adds an iteration of the Serpinski Triangle fractal. Face 1 = solid Face 2 = 3 solid triangles, 1 hole triangle Face 3 = 9 solid triangles, 4 hole triangles Face 4 = 27 solid triangles, 13 hole triangles Added Optional.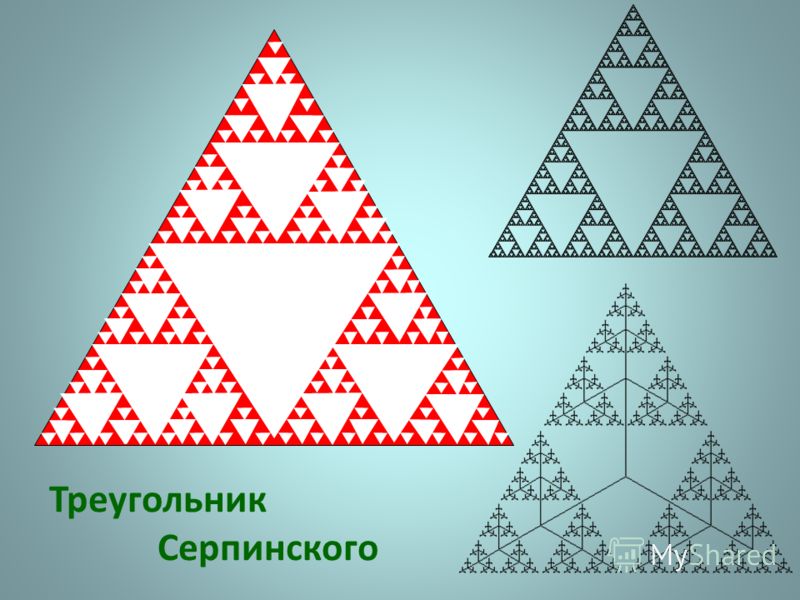
..
Sierpiński Pyramid Stacked
thingiverse
Remix of Fractal Pyramid: https://www.thingiverse.com/thing:1356547 .
5 level Sierpinski triangular pyramid
thingiverse
five level Sierpinski fractal triangular pyramid generated in Mandelbulb 3D
OpenSCAD Octahedron fractal
thingiverse
Fractal pyramid. With options. ...There are a variety of these available already but I wanted something that could easily be modified.
Sierpinski Pyramid
grabcad
Fractal Sierpinski Pyramid connected to each other. ...Mesh files created using Turbo Pascal programming, and rendered using ViViD raytracer
Fractional Pyramid Stand
thingiverse
Pyramid Stand for Fractal Pyramid with Continuous Cross-section designed ricktu. You can print two of the pyramids and glue them together to make an octahedron shape that the stand will then hold. ...I used pyramid6 in my stand.
FRACTAL
pinshape
fractal
FRACTAL
pinshape
fractal design
fractal
thingiverse
fractal, crop circle
Fractal
pinshape
Fractal j cube
3d Fractal - Etsy.
deEtsy is no longer supporting older versions of your web browser in order to ensure that user data remains secure. Please update to the latest version.
Take full advantage of our site features by enabling JavaScript.
Find something memorable, join a community doing good.
(563 relevant results)
Youtuber revives old-fashioned fractal vise using low-budget 3D printing
open source rare vintage fractal vise.
Unlike the standard straight vise, which can usually only clamp block-like parts, the century-old fractal design can transform to grip almost any object, no matter how complex the geometry. Dubbed "the coolest tool you never knew you had," a fractal vise is nearly impossible to buy these days - that's where low-cost FFF 3D printing comes in.
Teaching Tech stated, “My mind was blown. I had no idea such an incredible tool existed and I just needed to have my own. However, you can't just buy one, so I had to make my own. Luckily, I'm in a room surrounded by 3D printers."
In mathematics, fractals are complex geometric shapes containing endless patterns. When you zoom in on a fractal pattern, you see a smaller version of the original pattern, and the pattern is repeated over and over again (like an endless array of Russian nesting dolls).
A well-known example of fractal design is the Sierpinski pyramid model for 3D printing, which many in the fabrication community have no doubt encountered.
The pyramid consists of five smaller pyramids, each of which consists of five even smaller pyramids.
So, how does the concept of a fractal relate to a vice? The fractal vise actually consists of a series of stacked arcs, with each arc containing two smaller arcs that are half the diameter. The open source Teaching Tech project has four layers of these arcs, which means that each fractal vise jaw has eight arc grips that hold the part in place. In contrast, conventional vices have only two edges that cannot match the shape of the part between them.
When starting the project, Teaching Tech already had a number of specifications in mind for 3D printed vices. He wanted the vise to be able to grip almost any part geometry and restrict it to the point where it can't move. He also wanted to design them so that they could not rotate to the point of self-disassembly and wanted to minimize the use of supporting structures.
Teaching Tech's plan to avoid the use of support material was to cut each arc in half, leaving large cross-sections on smaller pieces.
It also helped make individual components easier to print and remove from the platform. The next problem was tightening the assembly to completely limit the clamped parts. To do this, he simply removed the set screw from the original design and replaced it with stoppers built into the 3D model itself.
Once 3D printed and assembled, the fractal vise "works great" to grip a lot of unconventional objects and secure them with ease. This includes a wrench, an artistic bust, and even a banana.
All open source STL files for fractal vises can be found here, and a video tutorial on the build process can be found here. While Teaching Tech did use PLA and TPU to 3D print the fractal vise, other polymer filaments will do as well.
Content Creator concludes: “What I really care about is how the community is accepting the design with remixes and tweaks. I have no doubt that the original metal version is superior to this one, but you just can't get one, so this democratic production means that anyone with a 3D printer can have their own copy of the vise.
"
The open source 3D printing community is often a source of great innovation, producing low-cost designs that you simply won't find in the industry. A YouTuber student named Lucas VRTech previously designed and 3D printed a pair of inexpensive finger-tracking gloves for use in virtual reality. The open-source gloves, called LucidVR, cost just $22 and give users the ability to accurately track their fingers without the need for special VR controllers.
Elsewhere, open source 3D printing enthusiast Johan von Konow previously launched a modular 3D printing MIDI synthesizer as a standalone project. Called the LEET Synthesizer, this fun project can be built for a total of $6 and only requires a few basic soldering and embedded electronics programming skills.
Source: 2757/
Project work on the topic "Fractals"
All-Russian Research project competition,
completed schoolchildren with scientific advice
scientists International Association of Construction Universities
Voronezh State Technical University
Section mathematics
Nomination Grade 10
Subject project Fractals
Babenko Stanislav Anatolyevich, (student of grade 10)
Kalacheevskaya School No.
6, Kalach
Supervisor: teacher mathematics secondary school №6, Kalach
Kashkina Antonina Vladimirovna
Scientific consultant: Glazkova Maria Yurievna Candidate of Physical and Mathematical Sciences, Associate Professor, Department of Applied Mathematics and Mechanics
glazkovam@yandex.
9000 9000 9000 9000
062
2021
Keyword list: fractals, geometric fractals, self-similarity, symmetry, 3D modeling, napkin and Sierpinski's pyramid, properties of a fractal polyhedron, surface area.
Annotation
Fractals project prepared using design technology.
In the process of working on a project, the author showed independence, used the search method and modeling considered the field of mathematics - fractal geometry, which appeared not so for a long time. The author showed the creation of models of geometric fractals on a 3D printer, thereby determined the scope of fractals with computer science and mathematics. As a result of the study, the author was convinced that the surface area fractal polyhedron tends to infinity. Thus, in In the work under consideration, the author showed the ability to understand the terms related to this topic, systematized the material and summarized it, thanks to which deepen school ideas about the topic under study.
This project may be used in extracurricular work in mathematics.
Table of contents……………………………………………………………………2 …………………………………2
Title sheet………………………………………………………………1
I. ………………………………………………………………3-4
II. Main part ……………………………………………………………4- 15
2.
1 The concept of a fractal. A bit of history ……………………………………………………………………………………………………………………………………………………………………………………………………………………………4-6
2.2 Geometric fractals …………………………………………………6-10
2.3 Research. "Modeling a Fractal Polyhedron - Pyramid Sierpinsky. surface area". …………………………………………………10- 15
III. Conclusion................................................. ................................................15
IV. List of used Literature………………………………………………………15-16
V. Applications.
Introduction.
Nature created objects that cannot be described using classical geometry. fractal geometry defines them very simply . Passed only a few decades since Benoit Mandelbrot declared: "Geometry nature is fractal!”, today we can already assume much more, namely that fractality is the primary principle of constructing all natural objects without exception.
[2,6]
My research project - "Fractals". In my opinion, this topic is new, as many the term "fractal" is heard for the first time. And no wonder Benoit Mandelbrot, father modern fractal geometry, introduced the term "fractal" in 1975, and the birth of vibrant fractal geometry dates back to 1977, when his book "The Fractal Geometry of Nature" whose materials I used in his work. The definition of a fractal given by Mandelbrot is as follows: "A fractal is a structure consisting of parts that in some way are similar to the whole in a sense. [4,5] In preparation for the defense of the project, I studied a lot of scientific popular literature, the list of which was indicated in the work.
Relevance my work is due, on the one hand, to the great interest in the topic "Geometric fractals" in modern science, and on the other hand, by the fact that in the school course geometry such a concept as "fractal" is not studied .
The subject of my research are fractals and a model of a fractal polyhedron - a pyramid Sierpinsky.
Purpose of research work:
explore a new direction mathematicians - geometric fractals.
Modeling fractal polyhedron "Sierpinski Pyramid" and calculation of its area surfaces.
In the course of my work, I the following research tasks are highlighted :
1. To study the history of the emergence of fractals.
2. Classify fractals.
3. Explore the properties of geometric fractals.
4. Simulate the Sierpinski Pyramid fractal polyhedron with help of a 3D printer.
5. Consider the properties of a fractal polyhedron. Display area its surface.
6. To give an idea of the fractals encountered in our lives.
7. Determine the areas of application of fractals with computer science and mathematics.
Hypothesis: The fractal body has a finite volume but an infinite area surfaces.
Methods research:
Analysis of scientific literature;
· Comparison of received data;
Modeling;
abstraction;
Execution and design research work using design technology and modeling.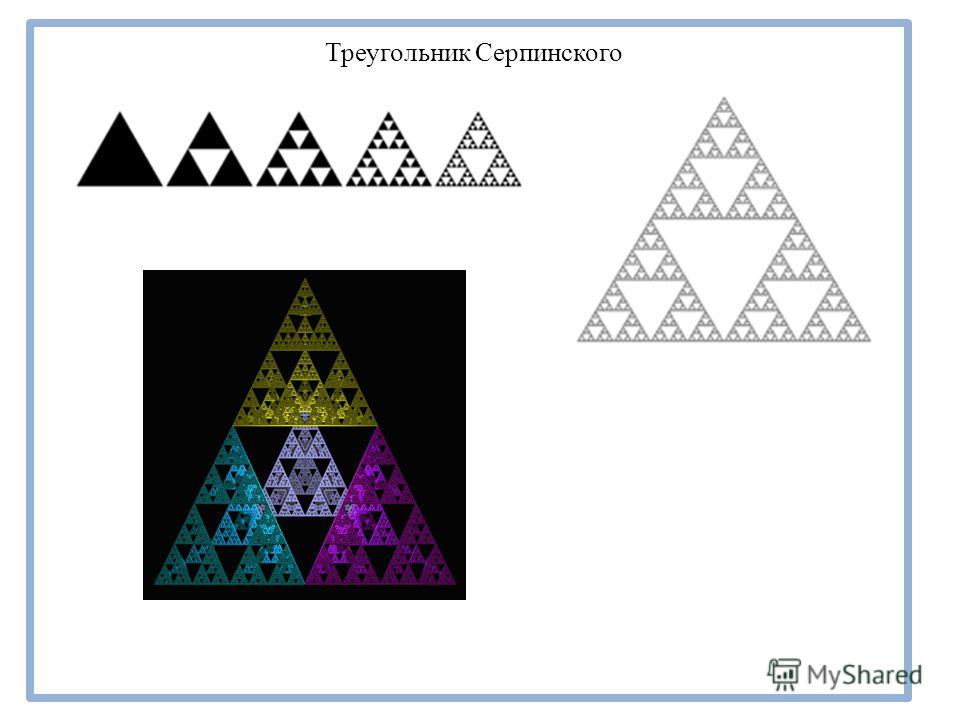
Main the method that was used in the work is the method of systematization and processing data and modeling.
Basic research results:
1. Increasing students' interest in fractal geometry.
2. Creating Models geometric fractals 3d printer assistance.
3. made sure that the area surface of the fractal polyhedron tends to infinity.
4. Calculate the surface area polyhedra depending on the steps.
5. Noticed a pattern in calculation of areas and derived the formula for the surface area of a fractal polyhedron.
6. Folder design, creation multimedia presentation.
2.1 . The concept of a fractal. A bit of history.
The first ideas of fractal geometries originated in the 19th century. Cantor with a simple recursive (repeating) procedure turned the line into a set of unconnected points (so called Kantor's Dust). He took the line and removed the central third and after this repeated the same with the remaining segments.
And so on ad infinitum. Her uniqueness in that it fills the entire plane. It has been proven that for each points on the plane, one can find a point belonging to the Peano line. Peano curve and Kantor's dust went beyond ordinary geometric objects. They didn't have clear dimension. Kantor's dust seemed to be built on the basis of a one-dimensional straight line, but consisted of points (dimension 0). And the Peano curve was built on the base of a one-dimensional line, and the result was a plane . [7,1]
However, their main elements are not available. direct observation. In this respect, they are fundamentally different from familiar objects of Euclidean geometry, such as a straight line or circle. Fractals are expressed not in primary geometric forms, but in algorithms, sets of mathematical procedures. These algorithms are transformed into geometric shapes using a computer. Repertoire of algorithmic elements inexhaustible. Having mastered the language of fractals, you can describe the shape of the cloud just as clearly and simply how an architect describes a building with drawings in which the language of traditional geometry is used [2,9]
From a mathematical point of view fractal (fraction, fractional - fraction, fractional) - this is primarily a set with a fractional dimension.
In Euclidean geometry, a point has dimension 0, a segment, and circle - dimension 1, circle and sphere - dimension 2.
Felix Hausdorff (1868-1942) in 1919 was the first to find in mathematics sets with a fractional dimension (Cantor set, Koch curve, etc.). [2,9] This direction was developed by Abram Samoylovich Besikovich (1891-1970), the Hausford-Besikovich dimension found application in some branches of mathematics, but a huge interest in it arose after publications at 1975 Benoit Mandelbrot (1924-2010) books (most famous edition of Benoit B. Mandelbrot//The Fractal Geometry of Nature Henry//Holt and Company, 1983, P. 468), in which he cited vivid examples of the use of fractals to explain some natural phenomena.
Fig.2.
The term "fractal" B. Mandelbrot introduced in 1975. He gave the following definition: a fractal (from the Latin "fractus" - fractional, broken, broken) is a structure, consisting of parts similar to the whole. The property of self-similarity distinguishes sharply fractals from objects of euclidean geometry.
Self-similar figures exist in micro and macro world. [2,3]
Fractals are divided into groups. The largest groups are:
- geometric fractals; (Appendix 1,2,3)
- algebraic fractals;( Appendix 5)
- stochastic fractals. (Appendix 6)
Geometric fractals - the most obvious, because they show self-similarity. This type of fractal obtained by simple geometric constructions. [7,2]
In the two-dimensional case, their obtained using some polyline (or surface in the three-dimensional case), called a generator. In one step of the algorithm, each of the segments that make up A broken line is replaced by a broken line - a generator, on an appropriate scale. AT as a result of the endless repetition of this procedure, a geometric fractal. It is with geometric fractals that their history began. This type fractals is obtained by simple geometric constructions. Usually when constructing these fractals, one proceeds as follows: a "seed" is taken - an axiom - a set segments on the basis of which the fractal will be built.
Next to this "seed" apply a set of rules that transforms it into some geometric figure. Further, to each part of this figure, the same set of rules. With each step, the figure will become more and more difficult, and if we spend (at least mentally) an infinite number of transformations - we get a geometric fractal (Appendix 1) This is how property characteristic of fractals self-similarity. In many works on fractals use self-similarity as a defining property. [7,6]
The dimension of is one of the fundamental concepts that goes far beyond mathematics. [4,1]
In our daily lives, we We are constantly dealing with dimensions. The line has dimension 1. This means that by choosing a reference point, we can determine any point on this line with with a single number, positive or negative. And this applies all lines - circle, square, parabola, etc. Dimension 2 means that any point can be uniquely identified by two numbers.
Thus the dimension D can be calculated based on the dependence of the increase in the “size” of the object S on increase in linear dimensions L.
D \u003d log (S) / log (L). If you try apply these rules to fractal objects, then a paradoxical situation - their dimension will be a fractional number. So, when the dimension of the figure, obtained from some simple objects (segments) is greater than the dimension of these objects - we are dealing with a fractal. [3,4]
Koch Curve - fractal curve, described in 1904 by the Swedish mathematician Helge von Koch.
Fig. 3. [6,3]
Initiator - straight line;
Generator - equilateral triangle .
The process of its construction looks like this:
Divide the unit segment into three equal parts and replace the middle an equilateral triangle interval without this segment. As a result a broken line is formed, consisting of four links of length 1/3. At the next step, we repeat the operation for each of the four resulting links, etc. The Koch curve is a non-self-intersecting continuous curve of infinite length that has no tangent at any point.
One version of this curve is called "Koch's snowflake" (Appendix 1).
The Levy curve was proposed by the French mathematician Levy, it turns out if take half of the square of the form / \, and then replace each side with the same fragment, and repeating this operation, in the limit we obtain the Levy curve (Appendix 2). The Levy curve is nowhere differentiable and not straightened. On any interval of the Levy curve there are points of self-intersection. Levy curve - crown of a tree Pythagoras.
Fig.4. [6,2]
Curve Minkowski — classic Geometric Fractal, suggested by Minkowski. The source element is a segment, and the generator is a polyline from eight links (two equal links continue each other) (Appendix 1).
Curve dragon
next: fold the strip of paper across in half. Let's repeat this a couple of times. After deployment, we get a strip consisting of eight pieces. Looking at this strip in profile, we will see a broken line.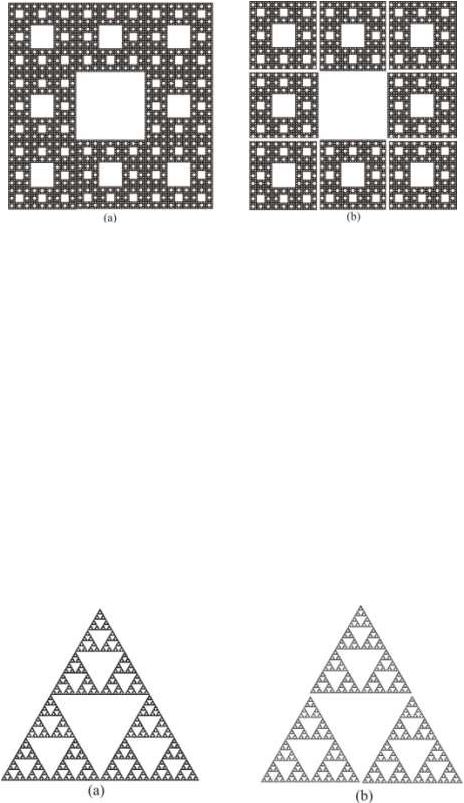
This can be continued, but very long, due to the finite thickness of the paper. Fig.5. [5,3]
Geometric plotting the dragon curve.
First we take segment of unit length. Then it is replaced by two segments forming lateral sides of an isosceles right triangle for which the original the segment is the hypotenuse. As a result, the segment seems to bend under right angle. The direction of the deflection alternates. The first section bends to the right, the second - to the left, the third - again to the right, etc. So after each step, the number of segments available is doubled, and the length of each decreases accordingly.
I. Sierpinski triangle.
Fractal, called Sierpinski's napkin (Sierpinski gasket), it turns out successive cutting out of the central ones as shown in the figure
But even on this Not all. It turns out that the Sierpinski triangle is obtained as a result of one of varieties of random walk of a point on a plane.
This method is called "Chaos game". It can also be used to construct some other fractals.
Game Chaos [6,3].
The essence of the "game" is as follows. fixed on the plane regular triangle A1A2A3. Mark any starting point B0. Then randomly choose one of the three vertices of the triangle and mark the point B1 - the middle of the segment with ends at this vertex and at B0 (in the figure on the right, by chance vertex A1 got out). The same is repeated with point B1 to get B2. Then they get points B3, B4, etc. It is important that the point “jumps” randomly. way, that is, that each time the vertex of the triangle is chosen randomly, regardless of what was selected in the previous steps. It's amazing that if mark points from the sequence Bi, then soon it will begin to show through Sierpinski triangle
Chaos game: 100, 500 and 2500 points [6,4].
Some properties
Fractal dimension log23 ≈ 1.584962....
The Sierpinski triangle consists of three copies of itself, each is half the size. Their mutual arrangement is such that if we reduce grid cells twice, then the number of squares intersecting with the fractal, will triple. The Sierpinski triangle has zero area. This means that in the fractal will not fit any, even a very small, circle. That is, if start from the construction in the first way, the entire interior: after each iteration, the area of what remains is multiplied by 3/4, that is, it gets smaller and tends to 0.
Options
II. Carpet (square, napkin) Sierpinsky.
Fig.7 [7,3].
The square version was described by Vaclav Sierpinsky in 1916. He was able to prove that any curve that can be draw on the plane without self-intersections, homeomorphic to some subset this holey square. Like a triangle, a square can be obtained from different structures. On the right is the classic way: dividing the square by 9parts and ejection of the central part.
Then the same is repeated for the remaining 8 squares, etc. Like a triangle, a square has zero square. The fractal dimension of the Sierpinski carpet is log38, calculated similar to the dimension of a triangle.
The square version was described by Vaclav Sierpinsky in 1916. He was able to prove that any curve that can be draw on the plane without self-intersections, homeomorphic to some subset this holey square. Like a triangle, a square can be obtained from different structures. On the right is the classic way: dividing the square by 9parts and ejection of the central part. Then the same is repeated for the remaining 8 squares, etc. [9,5]
III. Sierpinski Pyramid .
One of the three-dimensional analogues of a triangle Sierpinsky. It is built in a similar way, taking into account the three-dimensionality of what is happening: 5 copies of the initial pyramid, halved, make up the first iteration, its 5 copies make up the second iteration, and so on.
The fractal dimension is log25. At the figure zero volume (half of the volume is discarded at each step), but the area surface is preserved from iteration to iteration, and for a fractal it is the same as and at the initial pyramid. Fig.8. [6,6]
2.3. Research. "Modeling a fractal polyhedron - the Sierpinski pyramid. surface area".
Studying, modeling geometric fractals on a plane and looking at the “Sierpinski lattice”, I set a goal: to model the Sierpinski pyramid polyhedron and check the paradox of fractal structures (a fractal body has a finite volume, but infinite surface area).
In order to realize the task, I had to study additional topics: polyhedra, developments of convex polyhedra, area surfaces of regular polyhedra, modern geometry. Part of my research I started work by modeling a fractal polyhedron - a pyramid Sierpinsky at help of a 3D printer. (Annex 4)
The models created in the project were printed on a MakerBot printer Replicator Z18 installed in a school computer science lab.
MakerBot The Replicator Z18 is the fifth generation 3D printer. To print a model, designed in the Make Human program, size 70x200x55 to the printer it will take 2 hours 45 minutes and 30 grams of consumables, while there will be 1760 layers of PLA filament applied.
Fig.9.
Implementation:
Stages:
1) Creation of a 3D model of the Sierpinski pyramid fractal.
When creating the model, I used Tinkercad - this is a cross-platform software for creating and editing 3D projects.
This application allows you to make many types of 3D layout projects. The online format involves a quick exchange of models between users. Using the built-in tools, you can export projects for subsequent work in other more powerful editors or printing on 3D printers. In building the model, we need the "Pyramid" shape, with its when selected, an equilateral quadrilateral is set on the work plane pyramid, place it in this position:
Fig.9.
add three more pyramids and place them as follows:
Fig.
10.
place the fifth pyramid in such a way that its base is touched the tops of the four underlying pyramids, namely:
Fig.11.
copy the resulting structure, copy several times, place thus:
Fig.12. Fig.13
We repeat the operation several times and get the following construction:
Fig.14
I got a clear 3D model of the Sierpinski pyramid fractal. (Application 4)
Fig.15. fig.16
Surface area of the Sierpinski pyramid.
I will continue my research.
Purpose: To derive the formula for the surface of Sierpinski's fractal pyramid.
I. I will simulate the correct triangular pyramid (tetrahedron). We insert into it an octahedron whose edge is two times smaller than the edge of the pyramid. Note the four "hollow" pyramids formed. Insert into each of them an octahedron whose edge is also half the edge of the smaller one. pyramids.
Fig.17 This process can be continued until infinity.
Thus, it is possible to model a fractal polyhedron pyramid Sierpinsky, which has the property of self-similarity.
| Steps | 1 | 2 | 3 | 4 | 5 |
| Quantity octahedra | 1 | 1+4 | 1+4+16 | 1+4+16+64 | 1+4+16+64+256 |
| pattern numbers | 4 0 | 4 0 +4 1 | 4 0 +4 1 +4 2 | 4 0 +4 1 +4 2 +4 3 | 4 0 +4 1 +4 2 +4 3 +4 4 |
| Total octahedra | 1 | 5 | 21 | 85 | 341 |
Table 1.
The number of inscribed octahedra.
We notice that in pyramid with each step is added 4 n -1 octahedrons, that is, at the sixth step, 4 5 octahedra are added, at seventh step 4 6 octahedrons, etc.
Derivation of the recurrent formula for the number of octahedrons:
, means , etc. Recurrent formula:
II. Consider step by step changes edge lengths of octahedrons inscribed in a fractal polyhedron of a pyramid Serpinskog.
Table 2.
| step | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Octahedron edge length |
|
|
|
|
|
|
|
|
|
|
| Octahedron edge length |
|
|
|
|
|
|
|
|
|
|
Sequence numbers , , , .
. ,... there is an infinitely decreasing geometric progression, where = - the length of the edge of the first inscribed octahedron, .
III. Examining Surface Area Properties fractal polyhedron of the Sierpinski pyramid.
Hypothesis : Will the surface area of a regular fractal polyhedron be increase in inscribed octahedra, more surface area of the base pyramid fractal polyhedron?
If the edge of the first the octahedron inscribed in the pyramid is equal to , then the edge tetrahedron equals 2. And the surface area Sierpinski pyramids" - the basis of the fractal polyhedron is equal to:
(fig.18)
Area surface of a fractal polyhedron. Step first:
Area surface of a fractal polyhedron. Step Two:
Area surface of a fractal polyhedron. Step three:
that at the third step the surface area of the fractal polyhedron is greater than surface areas of the pyramid - the basis of the fractal polyhedron of the pyramid Sierpinsky.
The hypothesis has been proven.
Area surface of a fractal polyhedron. Step Four:
Table 3. Area increment:
| Step 1 | Step 2 | Step 3 | Step 4 | Step 5 |
| 0 |
|
|
| ? |
| 0 |
|
|
| ! |
On in the fifth step, the area will increase by
Table 4.
Areas of a fractal polyhedron depending on steps.
| steps | 1 | 2 | 3 | 4 | 5 |
| Area of a polyhedron |
|
|
|
|
|
Output: the formula for the area of a fractal polyhedron is . where
Paradox : despite the fact that the fractal polyhedron of the Sierpinski pyramid is limited tetrahedron, its surface area with increasing steps tends to infinity
IV.
Conclusion.
As a result of the research work, I proved the hypothesis that a fractal body has a finite volume but an infinite surface area. Were calculations were made and the formula for the surface area of the fractal polyhedron, the models of which I made from improvised means and using a 3D printer.
As a result of my research, I realized that models built on based on fractal images accurately describe the real world. Fractals are very as varied as their uses. As a result of my research, goals and objectives have been achieved. I studied scientific articles and materials about fractals from internet sources. I learned a lot of interesting things about these amazing objects, which help us understand the beauty of the world around us, I realized that the fractal geometry is the science of nature. The practical significance of the work lies in systematization of information about geometric fractals and attraction of interest to this topic. In the future, I will continue to study other types of fractals and their application.
It gives me pleasure to engage in modeling, thereby enriching myself with new discoveries.
v. List Literature:
1 Azevich A.I. Fractals: geometry and art // Mathematics at school - 2005. - No. 4. - P. 76-78.
2 Beckman I.N. Geometry fractals. Course of lectures//Moscow State University. M.V. Lomonosov//Moscow, 2010-p.1-29.
3 Demenok S.L. Just a fractal. - St. Petersburg: Strata LLC, 2014.
4 Mandelbrot B. Fractal geometry of nature. – Moscow: Institute for Computer Research, 2002. - 656 p.
5 Kacharava A.S. Living mathematics: Practical application of fractals in life // International school scientific bulletin. - 2019. - No. 5-1. – P. 59-67;
Internet resources:
6. https://elementy.ru/posters/fractals/Sierpinski
7. Sakva D.Yu. Fractals around us [Electronic resource] - Access mode. — URL: http://www.codenet.ru/progr/fract/Fractals-Around/
Applications
Applications 1.
